Cours chapitre 3 Physique
ETUDE DES EFFETS D'UN SYSTEME DISPERSIF SUR LA LUMIERE
Compétences :
Etablissement des lois de Descartes sur la réfraction pour une radiation lumineuse.
Repérer un angle entre un rayon lumineux et une référence.
Modélisation mathématique d'une loi physique.
Expression de la longueur d'onde, caractériqtique d'une radiation lumineuse
Dispersion de la lumière blanche par un prisme. Variation de l'indice de réfraction en fonction de la longueur d'onde
Dans un milieu homogène, la lumière se propage en ligne droite.
Cas de l'air + spray ou craie pour visualiser le faisceau lumineux.
Dans un milieu non homogène en concentration ou en température, la lumière ne se propage plus en ligne droite. Le faisceau lumineux est dévié.
Cas d'une variation de concentration
Cas des mirages (variation de température)
Activité 1 page 198
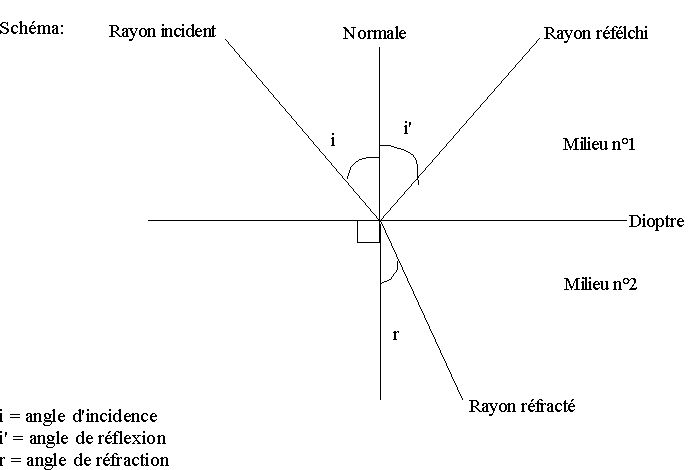
La surface de séparation entre deux milieux est appelée dioptre.
Le rayon peut être :
réfléchi (cas du miroir, surface lisse),
diffusé (cas d'une surface non lisse) c'est à dire réfléchi dans toutes les directions de l'espace)ou
réfracté ( il passe dans le second milieu translucide ou transparent)
La lumière a deux natures. Elle correspond au déplacement de photons (grains de matière sans masse) et en même temps à une onde électromagnétique. C'est un ensemble de radiations lumineuses dont chaque radiation correspond à une nuance de couleur visible ou non.
Dans l'air et dans le vide, on caractérise chaque radiation par sa longueur d'onde l exprimée en m ou en sous multiple du mètre.
L'ensemble des radiations émises par une source de lumière constitue un rayonnement. Si ce dernier n'est constitué que d'une seule radiation il est monochromatique (une seule couleur). S'il contient plusieurs radiations, il est polychromatique.
Les radiations lumineuses visibles sont comprises entre 400 et 800 nm
Voir documents 1 et 2 page 201
Le rayon incident, réfléchi et réfracté sont dans un seul et même plan, le plan d'incidence.

Remarque : le plan d'incidence est perpendiculaire à la surface de séparation des milieux car elle appartient au plan d'incidence
Soit une radiation de longueur d'onde l , elle se propage à une vitesse :
c dans le vide
v dans le milieu transparent étudié
L'indice de réfraction permet de traduire la différence existant entre le vide et ce milieu.
n = c / v
c et v étant exprimé en m/s, n est un nombre sans unité.
Remarque : c = 3,00.108m/s c'est la vitesse de la umière dans le vide, elle est valable pour toutes les radiations lumineuses. Ceci implique que c>v donc que c/v > 1 donc n > 1
Quelleque soit l, on prendra n = 1 pour le vide et n = 1, 000 pour l'air
Cf doc 4 p 202
Cf TP 3 de physique : la réfraction de la lumière
L'angle de réfraction est relié à l'angle d'incidence par la relation : n1 sin i = n2 sin r
n1 et n2 sont les indices de réfraction des milieux transparents 1 et 2 pour une radiation de longueur d'onde donnée.
Nous avons vu précédemment que le fait de chauffer l'air entrainait une déviation du faisceau lumineux. Lors de la formation d'un mirage, il est possible de considérer le milieu air comme une succession de fines couches d'air à une température donnée, donc ayant un indice de réfraction différent.
Un prisme est un solide transparent de base triangulaire. On étudie l'angle de déviation entre le rayon incident et le rayon émergent du prisme. Le rayon incident subit une première réfraction air/prisme puis une seconde réfraction prisme/air dans certaines conditions.

1ère réfraction :
Le rayon lumineux, passe d'un milieu moins réfringeant (air) à un milieu plus réfringeant (verre de flint) (n1<n2)
L'angle d'incidence est compris entre 0° et 90°
n1 = 1,000 donc comme n1 sin i1= n2 sin r1 et n1< n2 pour garantir l'égalité sin i1 > sin r1 donc i1 > r1
Le rayon réfracté se rapproche de la normale
2ème réfraction :
Le rayon lumineux, passe d'un milieu plus réfringeant (verre de flint) à un milieu moins réfringeant (air) (n2>n1)
L'angle de réfraction est compris entre 0° et 90°.
n2 sin i2 = n1 sin r2
Si r2 = 90° alors sin r2 =1 donc sin i2 = n1* 1 / n2 = n1/n2 or n2>n1 donc sin i2 < 1donc i2 peut être calculé.
Si l'angle d'incidence st plus grand que la valeur trouvée ci-dessus, on ne peut plus appliquer la 2ème loi de Descartes car à ce moment là, sin r2 > 1ce qui est impossible! Le rayon n'est plus réfracté mais totalement réfléchi. C'est le phénomène de réflexion totale.
Il faut que l'angle d'incidence à l'intérieur du prisme soit suffisamment faible pour ne pas entraîner une réflexion totale à l'intérieur du prisme. (Cf TP n °3 de Physique partie 8)
Si l'angle d'incidence st plus grand que la valeur trouvée ci-dessus, on ne peut plus appliquer la 2ème loi de Descartes car à ce moment là, sin r2 > 1ce qui est impossible! Le rayon n'est plus réfracté mais totalement réfléchi. C'est le phénomène de réflexion totale.

Le passage d'un rayonnement polychromatique dans une prisme disperse les différentes radiations qui le composent. On obtient un spectre composé de toutes les radiations présentes dans le rayonnement incident. Dans le cas de la lumière blanche, on obtient un spectre continu aux couleurs de l'arc-en-ciel.
Le prisme est un système dispersif car il permet la décomposition d'un faisceau polychromatique en une juxtaposition de faisceaux monochromatiques.
On remarque que les radiations les plus déviées sont celles qui ont les plus faibles longueurs d'onde. Le violet (l = 700 nm) est plus dévié que le rouge (l = 400 nm). Or la composition du prisme est la même quelleque soit la radiation. Donc l'indice de réfraction du prisme dépend de la longueur d'onde de la radiation qui le traverse. n = f(l)
Plus la variation de l'indice de réfraction avec la longueur d'onde est importante, plus le prisme est dispersif et plus le spectre est étalé (donc meilleure est la séparation des radiations.)
Rappel : La lumière blanche correspond à la somme des différentes radiations lumineuses présente dans le spectre obtenu.
Exemple : le réseau.
Il s'agit d'une diapositive comportant un très grand nombre de stries parallèles.