
LA REFRACTION DE LA LUMIERE
Etablir les lois de Descartes relatives à la réfraction
Réaliser un graphique permettant de modéliser une loi
Introduction de la notion d'indice de réfraction
un générateur 6-12V avec des fils électriques
une lanterne et des caches aimantés
un demi cylindre en plexiglas
un plateau
un disque rapporteur photocopié
Sur votre compte rendu, vous collerez le schéma fourni, vous lui donnerez un titre et vous le compléterez avec les mots appropriés se trouvant dans la liste fournie ci-dessous : (Il y a des intrus)
Voici la liste des mots à placer sur le schéma, les intrus sont barrés.
Rayon incident – Miroir – Transparent - Angle d'incidence – Normale - Rayon réfléchi - Angle de réfraction - Angle de réflexion - Surface de séparation – Dioptre – Lentille – Milieu n°1 – Air – Milieu n° 2 – Plexiglas – Rayon réfracté
Titre du schéma : plusieurs sont possibles mais il en faut un.
- Etude du passage de la lumière à travers la surface de séparation entre deux milieux (doc 5 p 203)
- Etude de la réfraction de la lumière,....
Réalisez le dispositif expérimental suivant.Vous prendrez garde à ne conserver qu'un faisceau lumineux très fin. Ce faisceau doit arriver au centre du demi-cylindre de plexiglas.
1/ Où lisez vous l'angle d'incidence? L'angle d'incidence se lit dans l'air entre la normale et le rayon incident.
2/ Où lisez vous l'angle de réfraction? L'angle réfracté se lit entre la normale et le rayon réfracté. Il se lit dans le demi cylindre ou à la sortie du rayon réfracté dans l'air. En effet tout rayon passant par le centre du demi-cylindre sort perpendiculaire à la surface de forme arrondi et n'est donc pas dévié (cf le cas d'un angle d'incidence nul)
Pour chaque valeur d'angle d'incidence demandé, vous mesurerez l'angle réfracté à 0,5° près et compléterez le tableau suivant. Vous recopierez le tableau obtenu sur votre compte-rendu.
|
Angle d'incidence en degré |
5 |
10 |
15 |
20 |
25 |
30 |
40 |
50 |
60 |
70 |
|---|---|---|---|---|---|---|---|---|---|---|
|
Angle de réfraction en degré |
3.5 |
6.5 |
10 |
13 |
16.5 |
19.5 |
25.5 |
30.5 |
35 |
39 |
1/ Le rayon lumineux entre dans le demi-cylindre au point I. Passe-t-il de l'air au plexiglas, ou du plexiglas à l'air? Le rayon lumineux incident est dans l'air puis passe dans le plexiglas au point I.
2/ Que vaut l'angle de réfraction quand l'angle d'incidence est nul? L'angle de réfraction est nul lorsque l'angle d'incidence est nul. Ce rayon n'est donc pas dévié.
3/ Lorsque l'angle d'incidence est important, le rayon incident se sépare en deux parties : le rayon réfracté et un autre rayon. A quoi peut bien correspondre cet autre rayon? L'autre rayon que l'on peut observer se trouve dans l'air et est le symétrique du rayon incident par rapport à la normale. Il s'agit du rayon réfléchi.
4/ Sur papier millimétré, placer dans un système d'axes (i en abscisse, r en ordonnée) les points correspondants à chaque couple de mesure.

5/ La modélisation par une droite de cet ensemble de point vous paraît-elle satisfaisante ? Argumentez. Lorsque l'on trace la courbe, il est possible de modéliser celle-ci par une droite pour des angles d'incidence petits. Cependant, plus on s'éloigne de la Normale et moins cette modélisation est satisfaisante, en effet les points relevés ne suivent plus la même loi de proportionnalité observée au début. Il est impossible de modéliser cette courbe par une droite unique.
6/ J. Kepler (1571-1630) jugea devant une série de mesures telle que la vôtre que la loi r = k*i pouvait assez bien convenir pour des petits angles. Déterminez dans quel intervalle de i cette loi te semble valable. Cette loi est valable pour un angle d'incidence compris entre 0° et 30°
7/ Descartes (1596-1650) formula une relation de proportionnalité entre les grandeurs sin(i) et sin(r) valable pour tous les angles d'une série de mesures. Faites un tableau reprenant sin i et sin r. Tracez la courbe sin(r) en fonction de sin(i). la modélisation par une droite de cet ensemble vous paraît-elle satisfaisante ?
| i (°) | 0 | 5 | 10 | 15 | 20 | 25 | 30 | 40 | 50 | 60 | 70 |
| sin (i) | 0 | 0.09 | 0.17 | 0.26 | 0.34 | 0.42 | 0.5 | 0.64 | 0.77 | 0.87 | 0.94 |
| r(°) | 0 | 3.5 | 6.5 | 10 | 13.5 | 16.5 | 19.5 | 25.5 | 30.5 | 35.5 | 39 |
| sin (r) | 0 | 0.06 | 0.11 | 0.17 | 0.23 | 0.28 | 0.33 | 0.43 | 0.51 | 0.58 | 0.63 |
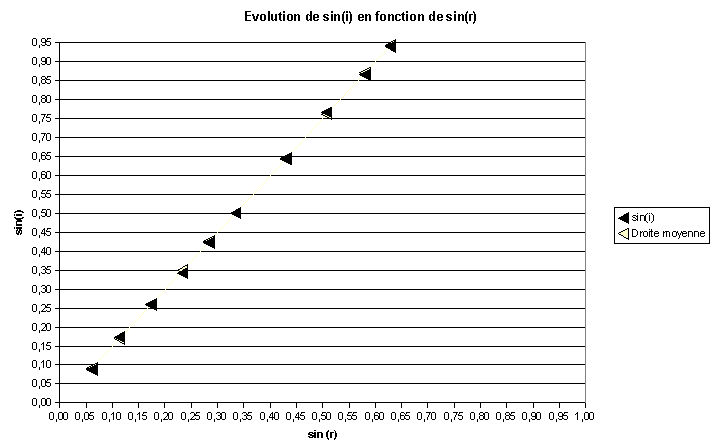
1/ Quelle est la relation entre i et r, traduisant pour tous les couples d'angles, le meilleur accord avec l'expérience ? sin (i) est proportionnel à sin (r ) donc on peut écrire :
sin(i) = k * sin(r) avec k coefficient de proportionnalité.
2/
Déterminez la pente (coefficient de
proportionnalité)
de la droite obtenue.
Il faut choisir deux points
appartenant à la droite moyenne. Le coefficient de
proportionnalité est obtenu par la formule : k = (y2-y1)/(x2-x1).
Soient le point M1 (x1;y1)= (0;0) et le point M2 (x2;y2) = (0.77;0.51), alors k = (0.77-0)/(0.51-0) = 1.5
3/
Comparer la valeur de la pente de la droite avec le rapport des indices de réfraction (indices entraînant des phénomènes optiques) des deux milieux considérés. (Données
: indice
de réfraction n1 de l'air = 1 ;
indice de
réfraction n2 du plexiglas = 1,5)
Cette valeur 1.5 correspond à l'indice de réfraction du
plexiglas ou au rapport (quotient) de l'indice de réfraction du
plexiglas par l'indice de réfraction de l'air.
4/
En déduire la relation entre sin(i), sin(r) et n = n2/n1.
Cette relation constitue la deuxième loi de Descartes. Soit n le coefficient de proportionnalité entre sin(i) et sin(r), on peut écrire n=k donc
sin (i) = n sin(r) or n = n2/n1 donc sin (i) = (n2/n1) sin(r) d'où la deuxième loi de Descartes :
n1 sin(i) = n2 sin(r)
Lorsque l'on passe d'un milieu moins réfringeant (indice de réfraction plus petit) à un milieu plus réfringeant (indice de réfraction plus grand), le rayon réfracté se rapproche de la normale.
NB: Existe t'il un angle limite de réfraction ?
On a vu que pour un angle d'incidence nul, l'angle de réfraction est nul. Que se passe t il si l'angle d'incidence est perpendiculaire à la normale?
sin (i) < 1 par définition donc i < 90° donc n1 sin(i) <1 donc n2 sin (r) < 1 soit sin (r) < 1/n2 donc sin(r) < 0.66 donc r < 41.8°.
Il est impossible d'obtenir un angle réfracté supérieur à 41.8°
1/ Reprenez le dispositif précédent en faisant maintenant entrer la lumière par la face cylindrique du demi cylindre. Effectuez une série de 6 mesures que vous traiterez de la même manière.
Cette fois-ci, on colle la source lumineuse contre la partie arrondie du demi-cylindre de manière à ce que le rayon arrive au point I , point d'incidence et centre du demi-cercle. On crée ainsi un rayon incident à travers le plexiglas. Ce rayon passe dans l'air au point I . Le rayon réfracté se trouve dans l'air.
| i (°) | 0 | 10 | 20 | 30 | 40 | 50 | 60 |
| r (°) | 0 | 15.1 | 30.9 | 48.6 | 74.6 | Impossible | Impossible |
| sin (i) | 0 | 0.17 | 0.34 | 0.5 | 0.64 | 0.77 | 0.87 |
| sin (r) | 0 | 0.26 | 0.51 | 0.75 | 0.96 | Impossible | Impossible |
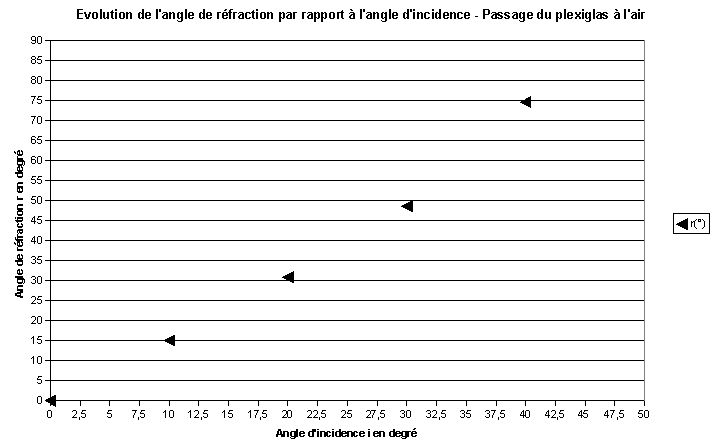
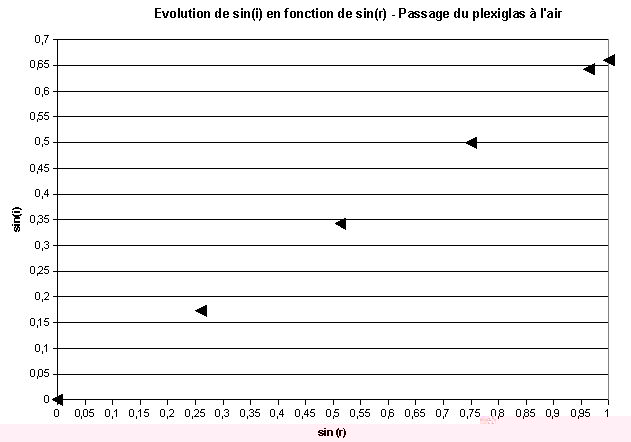
A partir d'un certain angle il n'y a plus de réfraction. On atteint la limite de réfraction quand r vaut 90°.
Il
est possible de calculer pour quel angle d'incidence cette valeur sera
atteinte. Pour r = 90° , j'applique la deuxième loi de
Descartes avec cette fois-ci : n1 indice de réfraction du milieu 1 le plexiglas (1.5) et n2 indice de réfraction du milieu 2 l'air (1)
n1 sin(i) = n2 sin(r) donc sin(i) = (n2/n1)
sin(r) = 1/1.5 * 1 = 0.66 soit i = 41.8° Au dela le rayon incident
n'est plus réfracté (sin(r)>1 est impossible). On est
dans le cas de la réflexion totale. Ce phénomène
n'est possible que si l'on passe d'un milieu plus réfringeant
à un milieu moins réfringeant.
2/ Imaginez une expérience permettant de déterminer l'indice de réfraction d'un milieu transparent quelconque. Réalisez-la avec comme deuxième milieu transparent l’eau dont l’indice de réfraction vaut n2 = 1,33.
Il suffit de placer à la place du demi-cylindre en plexiglas une cuve remplie d'eau. Il faut que cette cuve soit suffisamment large pour pouvoir déterminer avec précision l'angle de réfraction. L'idéal est d'utiliser une cuve en forme de demi-cylindre pour retrouver les conditions de la première expérience.